Answer:
7, 9
Explanation:
Let x and y represent the two positive integers.
We can write x in terms of y. The question states "one positive integer is 5 less than twice another". Let "one positive integer" represent x.
Therefore:
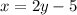
We also know that the sum of the squares of the two positive integers is 130. Using this information, we can write another equation.
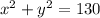
These two equations form a system of equations.
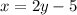
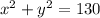
We can solve this system of equations by the substitution method. Using this method, we substitute
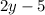 for
for
 .
.
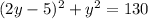
Expand
 . Notice that
. Notice that
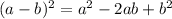 :
:
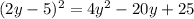
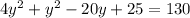
Subtract 25 from both sides
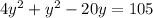
Add like terms
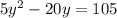
Divide both sides by 5
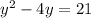
Subtract 21 from both sides
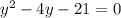
Factor the equation
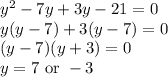
Since the question states that the two integers are positive, one of the integers is 7.
We can use this information to find the other integer.
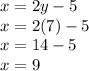
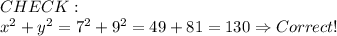
Therefore the two integers are 7 and 9.