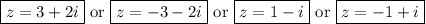Using the quadratic formula, we solve for
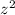 .
.
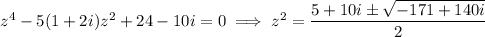
Taking square roots on both sides, we end up with
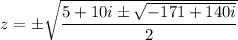
Compute the square roots of -171 + 140i.
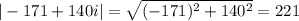

By de Moivre's theorem,
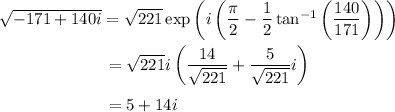
and the other root is its negative, -5 - 14i. We use the fact that (140, 171, 221) is a Pythagorean triple to quickly find
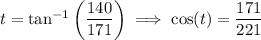
as well as the fact that
![0<\tan(t)<1 \implies 0along with the half-angle identities to find</p><p>[tex]\cos\left(\frac t2\right) = \sqrt{\frac{1+\cos(t)}2} = (14)/(√(221))](https://img.qammunity.org/2023/formulas/mathematics/college/ozgk2mevb82tt5yqvfsakv4nuj37fcbyj2.png)
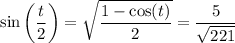
(whose signs are positive because of the domain of
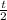 ).
).
This leaves us with

Compute the square roots of 5 + 12i.

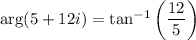
By de Moivre,
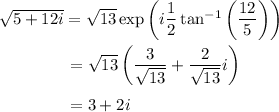
and its negative, -3 - 2i. We use similar reasoning as before:
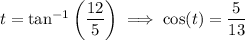
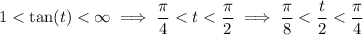

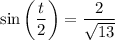
Lastly, compute the roots of -2i.
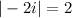
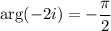
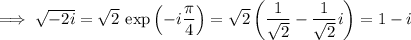
as well as -1 + i.
So our simplified solutions to the quartic are