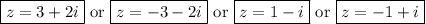Question

Z^4-5(1+2i)z^2+24-10i=0

Find the value of z.

Can someone please help me with this one?

Answer 1

Using the quadratic formula, we solve for
`z^2`.

`z^4 - 5(1+2i) z^2 + 24 - 10i = 0 \implies z^2 = \frac{5+10i \pm √(-171+140i)}2`

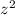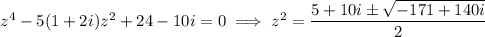
Taking square roots on both sides, we end up with

`z = \pm \sqrt{\frac{5+10i \pm √(-171+140i)}2}`

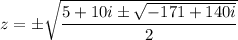
Compute the square roots of -171 + 140i.

`|-171+140i| = √((-171)^2 + 140^2) = 221`

`\arg(-171+140i) = \pi - \tan^(-1)\left((140)/(171)\right)`

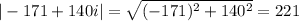
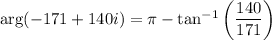
By de Moivre's theorem,

`√(-171 + 140i) = √(221) \exp\left(i \left(\frac\pi2 - \frac12 \tan^(-1)\left((140)/(171)\right)\right)\right) \\\\ ~~~~~~~~~~~~~~~~~~~~= √(221) i \left((14)/(√(221)) + \frac5{√(221)}i\right) \\\\ ~~~~~~~~~~~~~~~~~~~~= 5+14i`

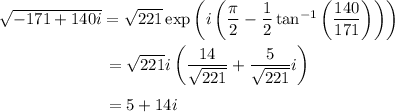
and the other root is its negative, -5 - 14i. We use the fact that (140, 171, 221) is a Pythagorean triple to quickly find

`t = \tan^(-1)\left((140)/(171)\right) \implies \cos(t) = (171)/(221)`

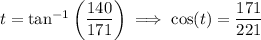
as well as the fact that

`0<\tan(t)<1 \implies 0along with the half-angle identities to find</p><p>[tex]\cos\left(\frac t2\right) = \sqrt{\frac{1+\cos(t)}2} = (14)/(√(221))`

`\sin\left(\frac t2\right) = \sqrt{\frac{1-\cos(t)}2} = \frac5{√(221)}`

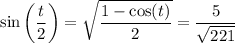
(whose signs are positive because of the domain of
`\frac t2`).

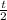This leaves us with

`z = \pm \sqrt{\frac{5+10i \pm (5 + 14i)}2} \implies z = \pm √(5 + 12i) \text{ or } z = \pm √(-2i)`

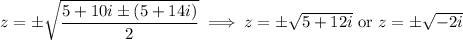
Compute the square roots of 5 + 12i.

`|5 + 12i| = √(5^2 + 12^2) = 13`

`\arg(5+12i) = \tan^(-1)\left(\frac{12}5\right)`

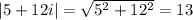
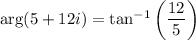
By de Moivre,

`√(5 + 12i) = √(13) \exp\left(i \frac12 \tan^(-1)\left(\frac{12}5\right)\right) \\\\ ~~~~~~~~~~~~~= √(13) \left(\frac3{√(13)} + \frac2{√(13)}i\right) \\\\ ~~~~~~~~~~~~~= 3+2i`

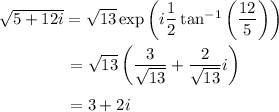
and its negative, -3 - 2i. We use similar reasoning as before:

`t = \tan^(-1)\left(\frac{12}5\right) \implies \cos(t) = \frac5{13}`

`1 < \tan(t) < \infty \implies \frac\pi4 < t < \frac\pi2 \implies \frac\pi8 < \frac t2 < \frac\pi4`

`\cos\left(\frac t2\right) = \frac3{√(13)}`

`\sin\left(\frac t2\right) = \frac2{√(13)}`

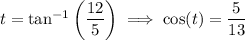
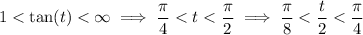
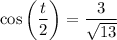
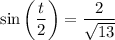
Lastly, compute the roots of -2i.

`|-2i| = 2`

`\arg(-2i) = -\frac\pi2`

`\implies √(-2i) = \sqrt2 \, \exp\left(-i\frac\pi4\right) = \sqrt2 \left(\frac1{\sqrt2} - \frac1{\sqrt2}i\right) = 1 - i`

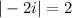
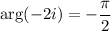
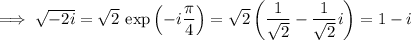
as well as -1 + i.

So our simplified solutions to the quartic are

`\boxed{z = 3+2i} \text{ or } \boxed{z = -3-2i} \text{ or } \boxed{z = 1-i} \text{ or } \boxed{z = -1+i}`