

❍ Arrange the given data in order either in ascending order or descending order.
2, 3, 4, 7, 9, 11
❍ Number of terms in data [n] = 6 which is even.
As we know,
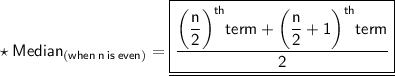

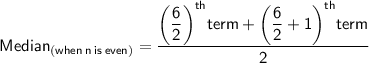

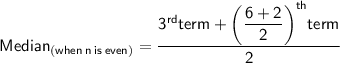

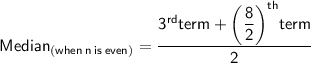

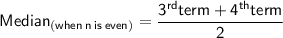
• Putting,
3rd term as 4 and the 4th term as 7.






❍ Arrange the given data in order either in ascending order or descending order.
1, 2, 3, 4, 5, 6, 7
❍ Number of terms in data [n] = 7 which is odd.
As we know,
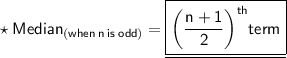

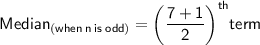

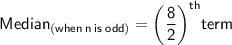


• Putting,
4th term as 4.
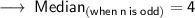



The frequency distribution table for calculations of mean :
![\begin{gathered}\begin{array}c \hline \rm x_(i) &\rm 3&\rm 1&\rm 7&\rm 4&\rm 6&\rm 2 \rm \\ \hline\rm f_(i) &\rm 4&\rm 6&\rm 2&\rm 2 & \rm 1&\rm 1 \\ \hline \rm f_(i)x_(i) &\rm 12&\rm 6&\rm 14&\rm 8&\rm 6&\rm \rm 2 \\ \hline \end{array} \\ \end{gathered}]()
☆ Calculating the

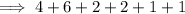
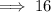
☆ Calculating the
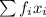
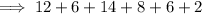
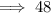
As we know,
Mean by direct method :
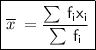
here,
•
 = 16
= 16
•
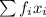 = 48
= 48
By putting the values we get,
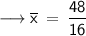
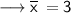

• Swipe to see the full answer.
