4. Compute the derivative.

Find when the gradient is 7.
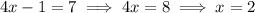
Evaluate
 at this point.
at this point.
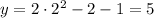
The point we want is then (2, 5).
5. The curve crosses the
 -axis when
-axis when
 . We have
. We have
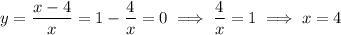
Compute the derivative.
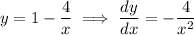
At the point we want, the gradient is
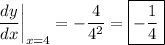
6. The curve crosses the
 -axis when
-axis when
 . Compute the derivative.
. Compute the derivative.

When
 , the gradient is
, the gradient is

7. Set
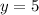 and solve for
and solve for
 . The curve and line meet when
. The curve and line meet when
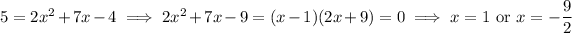
Compute the derivative (for the curve) and evaluate it at these
 values.
values.
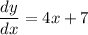
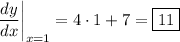
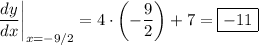
8. Compute the derivative.
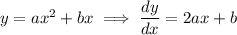
The gradient is 8 when
 , so
, so
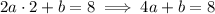
and the gradient is -10 when
 , so
, so
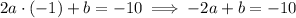
Solve for
 and
and
 . Eliminating
. Eliminating
 , we have
, we have
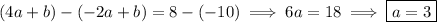
so that
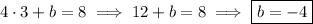 .
.