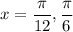Answer:
Explanation:
We are given the trigonometric equation of:
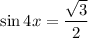
Let u = 4x then:

Find a measurement that makes sin(u) = √3/2 true within [0, π) which are u = 60° (π/3) and u = 120° (2π/3).
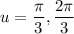
Convert u-term back to 4x:
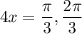
Divide both sides by 4:
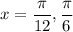
The interval is given to be 0 ≤ 4x < π therefore the new interval is 0 ≤ x < π/4 and these solutions are valid since they are still in the interval.
Therefore: