Question

a two digit number has twice as many ones as tens twice the original number is 9 more than the reversed number find the original number

Answer 1

Answer: 36

Explanation:

As this is a two-digit number, it will have a digit in its 10's place and a digit in its 1's place. We can represent the 10's digit using x and the 1's digit using y.

Since the ones is twice the number of tens, this means that y is equal to 2*x. Let's put this into an equation.

`y=2x`

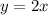
If the 10's digit is x and the 1's digit is y, the original number would be
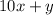`10x + y`, as x must be multiplied by 10 to get it to the 10's place. Similarly, the reversed number would be
`10y + x`, as y must be multiplied by 10 to get it to the 10's place.

Twice the original number (10x+y) is equal to 9 more than (i.e. 9 plus) the reversed number. We can put this into an equation to help us answer the question.

`2(10x+y)=9+10y+x\\20x+2y=9+10y+x\\19x+2y=9+10y\\19x=9+8y`

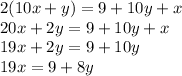
Now we have a system of two equations.

`y=2x\\19x=9+8y`

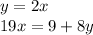
We can solve this system by substituting y for 2x in the second equation. Then, we can isolate and get the value of x.

`19x=9+8(2x)\\19x=9+16x\\3x=9\\x=3`

Now that we have the value of x, let's put it back into the first equation and solve for y.

`y=2(3)\\y=6`

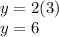
Remember that x is the 10's digit and y is the one's digit of our answer. Since x is 3 and y is 6, our answer is 36.

Checking

We can quickly check if our answer is right by making sure both conditions in the question are met.

6 (the one's digit) is twice the value of 3 (the ten's digit), making the first condition true. Twice of 36 is 72, which is 9 more than the reversed number, which is 63.