Question

Find all the frist differnce and explian your answer

Answer 1

Answer: No this is not a linear function as the y values have different first differences.

Explanation:

First we look at the x values. We start off and look at the second x value and subtract the first x value from it (That would be 1-0) and that equals to 1. Then we look at the third x value and subtract the second x value from it (2-1) and that equals to 1. Then we look at the fourth x value and subtract the third x value from it (That would be 3-2) and that is 1. Next we look at the fifth x value and subtract the fourth x value from it (That would be 4-3) and that is 1.

Now we look at the y values and do the same thing as with the x values. We start off and look at the second y value and subtract the first y value from it (That would be 1-0) and that equals to 1. Then we look at the third y value and subtract the second y value from it (4-1) and that equals to 3. Then we look at the fourth y value and subtract the third y value from it (That would be 9-4) and that is 5. Next we look at the fifth y value and subtract the fourth y value from it (That would be 16-9) and that is 7.

Even though the x values all have the same first differences, the y values do not and so this cannot be a linear function.

I hope this helps. Tell me if something doesn't make sense.

Answer 2

No, it is a quadratic relation.

Explanation:

Work out the first differences between the given y-values:

`0 \underset{+1}{\longrightarrow} 1 \underset{+3}{\longrightarrow} 4 \underset{+5}{\longrightarrow} 9 \underset{+7}{\longrightarrow} 16`

As the first differences are not the same, this is not a linear relation.

Work out the second differences:

`1 \underset{+2}{\longrightarrow} 3\underset{+2}{\longrightarrow}5\underset{+2}{\longrightarrow}7`

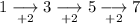
As the second differences are the same, the relation is quadratic and will contain an x² term. The coefficient of x² is always half of the second difference. As the second difference is 2, the coefficient of x² is one.

`\begin{array}c\cline{1-6}x & 0 & 1 & 2 & 3 & 4\\\cline{1-6}x^2 & 0 & 1 & 4 & 9 & 16\\\cline{1-6}\end{array}`

Comparing x² with the given y-values, we can see that no further operation is needed. Therefore, the relation is quadratic and the equation is
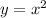`y=x^2`.