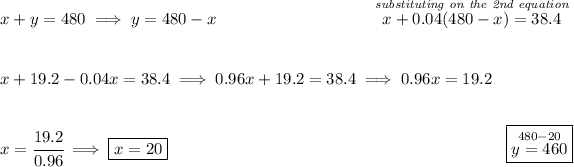Question

How many ounces of 100% acid solution should be combined with a 4% acid solution to obtain 480 ounces of an 8% acid solution

Answer 1

x = oz of 100% acid

y = oz of 4% acid

the first solution is 100% acid, if the amount of ounces in it is "x", how much only acid is there? well, (100/100) * x = 1.0x.

likewise, how much only acid is there in the 4% solution? well, (4/100) * y = 0.04y.

`\begin{array}{lcccl} &\stackrel{\stackrel{oz}{solution}}{quantity}&\stackrel{\textit{\% of }}{amount}&\stackrel{\textit{oz of acid }}{amount}\\ \cline{2-4}&\\ \textit{first solution}&x&1.00&1.0x\\ \textit{second solution}&y&0.04&0.04y\\ \cline{2-4}&\\ mixture&480&0.08&38.4 \end{array}~\hfill \begin{cases} x+y=480\\\\ x+0.04y=38.4 \end{cases}`

`x+y=480\implies y=480-x~\hfill \stackrel{\textit{substituting on the 2nd equation}}{x+0.04(480-x)=38.4} \\\\\\ x+19.2-0.04x=38.4\implies 0.96x+19.2=38.4\implies 0.96x=19.2 \\\\\\ x=\cfrac{19.2}{0.96}\implies \boxed{x=20}~\hfill \boxed{\stackrel{480-20}{y=460}}`