Answer:
no
Explanation:
So you can express a polynomial in factored form as such:
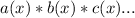 where a(x), b(x), and c(x), each represent a polynomial which are each factors of the equation. It's important to note that each factor is being multiplied by each other, meaning if any of the factors output 0, the entire thing is 0, no matter the value of the other factors, since 0 * some value = 0. For this reason, if we plug in the value that makes (x+1) 0, into the polynomial, and the polynomials value is 0, that means it is a factor.
where a(x), b(x), and c(x), each represent a polynomial which are each factors of the equation. It's important to note that each factor is being multiplied by each other, meaning if any of the factors output 0, the entire thing is 0, no matter the value of the other factors, since 0 * some value = 0. For this reason, if we plug in the value that makes (x+1) 0, into the polynomial, and the polynomials value is 0, that means it is a factor.
x + 1 = 0
x = -1
The value that makes the factor 0, is -1. This means that if it is a factor of the polynomial, then plugging in -1 as x into the polynomial should make the value 0.
Original Equation:
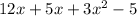
Plug in -1 as x
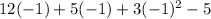
Multiply values
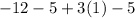
Simplify:
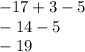
Since the value of the polynomial is not 0, this means x+1 is not a factor
You can also solve this use the Remainder Theorem and Factor Theorem which essentially uses the same logic
Remainder Theorem:
If a polynomial P(x) is divided by x-a, the remainder is P(a)
Using the remainder theorem, if x-a is indeed a factor, then that means the remainder should be 0, just as 11 is a factor of 77, and 77/11 has a remainder of 0. This is what the factor theorem essentially states
Factor Theorem:
The expression "x-a" is a factor of P(x) if and only if P(a) = 0