Let
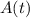 = amount of salt (in pounds) in the tank at time
= amount of salt (in pounds) in the tank at time
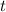 (in minutes). Then
(in minutes). Then
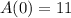 .
.
Salt flows in at a rate
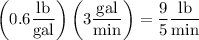
and flows out at a rate
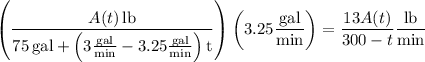
where 4 quarts = 1 gallon so 13 quarts = 3.25 gallon.
Then the net rate of salt flow is given by the differential equation
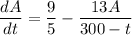
which I'll solve with the integrating factor method.
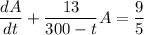
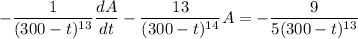
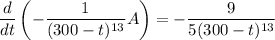
Integrate both sides. By the fundamental theorem of calculus,
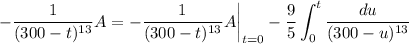
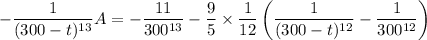
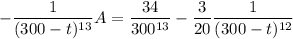
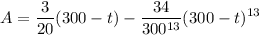
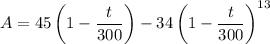
After 1 hour = 60 minutes, the tank will contain
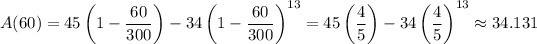
pounds of salt.