Question

A 75-gallon tank is filled with brine (water nearly saturated with salt; used as a preservative) holding 11 pounds of salt in solution. A salt solution containing 0.6 pounds of salt per gallon is added to the tank at the rate of 3gal/min. The contents of the tank are continuously and thoroughly mixed and drained out at thirteen quarts per minute. What is the amount of salt in the tank after an hour

Answer 1

Let
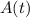`A(t)` = amount of salt (in pounds) in the tank at time
`t` (in minutes). Then
`A(0) = 11`.

Salt flows in at a rate

`\left(0.6(\rm lb)/(\rm gal)\right) \left(3(\rm gal)/(\rm min)\right) = \frac95 (\rm lb)/(\rm min)`

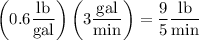
and flows out at a rate

`\left((A(t)\,\rm lb)/(75\,\rm gal + \left(3(\rm gal)/(\rm min) - 3.25(\rm gal)/(\rm min)\right)t)\right) \left(3.25(\rm gal)/(\rm min)\right) = (13A(t))/(300-t) (\rm lb)/(\rm min)`

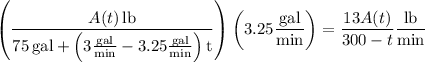
where 4 quarts = 1 gallon so 13 quarts = 3.25 gallon.

Then the net rate of salt flow is given by the differential equation

`(dA)/(dt) = \frac95 - (13A)/(300-t)`

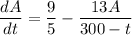
which I'll solve with the integrating factor method.

`(dA)/(dt) + (13)/(300-t) A = \frac95`

`-\frac1{(300-t)^(13)} (dA)/(dt) - (13)/((300-t)^(14)) A = -\frac9{5(300-t)^(13)}`

`\frac d{dt} \left(-\frac1{(300-t)^(13)} A\right) = -\frac9{5(300-t)^(13)}`

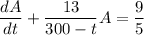
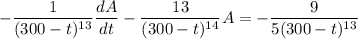
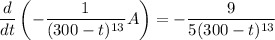
Integrate both sides. By the fundamental theorem of calculus,

`\displaystyle -\frac1{(300-t)^(13)} A = -\frac1{(300-t)^(13)} A\bigg|_(t=0) - \frac95 \int_0^t (du)/((300-u)^(13))`

`\displaystyle -\frac1{(300-t)^(13)} A = -(11)/(300^(13)) - \frac95 * \frac1{12} \left(\frac1{(300-t)^(12)} - \frac1{300^(12)}\right)`

`\displaystyle -\frac1{(300-t)^(13)} A = (34)/(300^(13)) - \frac3{20}\frac1{(300-t)^(12)}`

`\displaystyle A = \frac3{20} (300-t) - (34)/(300^(13))(300-t)^(13)`

`\displaystyle A = 45 \left(1 - \frac t{300}\right) - 34 \left(1 - \frac t{300}\right)^(13)`

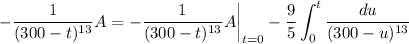
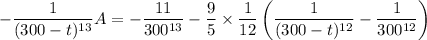
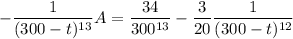
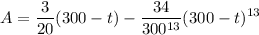
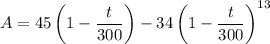
After 1 hour = 60 minutes, the tank will contain

`A(60) = 45 \left(1 - \frac {60}{300}\right) - 34 \left(1 - \frac {60}{300}\right)^(13) = 45\left(\frac45\right) - 34 \left(\frac45\right)^(13) \approx 34.131`

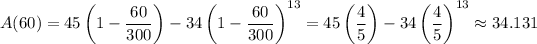
pounds of salt.