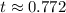Question

18 *2^5t = 261 what is the solution of the equation

Answer 1

0.772

Explanation:

Original equation:

`18 * 2^(5t)=261`

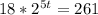
Divide both sides by 18

`2^(5t) = 14.5`

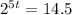
Rewrite in logarithmic form (
`b^x=c \implies log_bc=x`)

`log_214.5 = 5t`

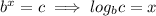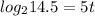
Divide both sides by 5

`(log_214.5)/(5)=t`

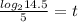
Rewrite the equation so that base is 10 using change of base formula:
`log_ba = (log_na)/(log_nb)`

`(((log14.5)/(log2)))/(5)=y`

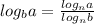
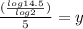
Keep, change, flip

`(log14.5)/(log2)*(1)/(5) = (log14.5)/(5 * log2)`

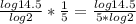
Use a calculator to approximate log14.5 and log2

`(1.161368)/(5 * 0.301029996) = t`

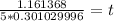
Multiply in denominator

`(1.161368)/(1.505149978) = t`

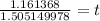
Divide two values

`t\approx 0.771596`

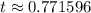
Round to nearest thousandth

`t\approx 0.772`