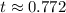Answer:
0.772
Explanation:
Original equation:

Divide both sides by 18
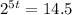
Rewrite in logarithmic form (
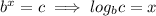 )
)
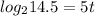
Divide both sides by 5

Rewrite the equation so that base is 10 using change of base formula:
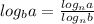
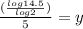
Keep, change, flip

Use a calculator to approximate log14.5 and log2
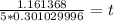
Multiply in denominator
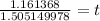
Divide two values
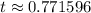
Round to nearest thousandth