Question

Please help meeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeee

Answer 1

Step-by-step explanation:

a) The quadratic formula can help find answers to a quadratic equation when it is equal to 0. The formula is
`x=(-b\pm√(b^2-4ac))/(2a)` for a quadratic equation of the form
`ax^2+bx+c=0`.

In this question, a is 5, b is -6, and c is -2. Let's put them in the equation and solve.

`x=(6\pm√((-6)^2-4(5)(-2)))/(2(5))\\x=(6\pm√(36+40))/(10)\\x=(6\pm√(76))/(10)\\x=(6\pm2√(19))/(10)\\x=(3\pm√(19))/(5)`

This means that the value of x is both
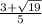`\frac{3+√(19)}5` and
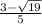`\frac{3-√(19)}5`, since both values make x equal to 0. Putting both into the calculator, we get that
`x=1.5` or
`x=-0.3`.

b) We can easily solve this equation using factoring, which turns a quadratic into two factors, and finds the solutions by setting both to 0. This will only work if the quadratic is equal to 0.

`x^2+3x-40=0`

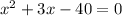
Now, we have to find two numbers that add to 3 and multiply to -40. The numbers 8 and -5 work, as 8-5=3 and 8*-5 is -40.

we can now make our factors x+8 and x-5

`(x+8)(x-5)=0`

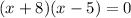
If two numbers, say A and B, are being multiplied and equal 0, then either A is 0, or b is 0, or both. Similarly, if x+8 and x-5 are being multiplied and equal 0, either x+8 = 0, or x-5=0.

`x+8=0\\x=-8`
`x-5=0\\x=5`

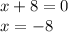
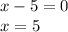
This makes our solutions x=-8 and x=5.

If you are not familiar with factoring or the process I have went through above, I highly recommend learning about it.

Answer 2

a) x = 1.5 or x = -0.3

b) x = 5 or x = -8

Step-by-step explanation:

Quadratic formula:

`\sf x = ( -b \pm √(b^2 - 4ac))/(2a) \quad when \:\: ax^2 + bx + c = 0`

Here given equation: 5x² - 6x - 2 = 0

Identify variable constants: a = 5, b = -6, c = -2

Putting these values into equation:

`\sf x = ( -(-6) \pm √((-6)^2 - 4(5)(-2)))/(2(5))`

`\sf x = ( 6 \pm √(36 + 40))/(10)`

`\sf x = ( 6 \pm √(76))/(10)`

`\sf x = ( 3\pm √(76))/(5)`

`\sf x = ( 3+ √(76))/(5) \quad or \quad ( 3- √(76))/(5)`

In one decimal point:

`\sf x = 1.5 \quad or \quad -0.3`

b) Here use "middle term split" method

⇒ x² + 3x = 40

relocate

⇒ x² + 3x - 40 = 0

The factors of 40 are 8 and 5

⇒ x² + 8x - 5x - 40 = 0

factor common terms

⇒ x(x + 8) - 5(x + 8) = 0

collect into groups

⇒ (x - 5)(x + 8) = 0

set to zero

⇒ x - 5 = 0 or x + 8 = 0

relocate

⇒ x = 5 or x = -8