Answer: 122°
Explanation:
∠1 an ∠2 are alternate interior angles, which are angles that are inside both parentheses and are on alternate sides of the transversal. The Alternate Interior Angles Theorem states that if two lines are parallel and cut by a transversal, then the alternate interior angles formed are congruent.
Since the lines are parallel as given in the question, ∠1 and ∠2 are of equal measure. We can solve for ∠2 by first solving for x, then plugging it in ∠2's measure.

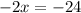
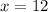
Putting x in the expression 12x-22, we get
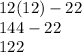
Hence, the value of ∠2 is 122°.