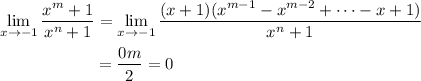I assume
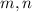 are integers to avoid (ir)rational powers of -1.
are integers to avoid (ir)rational powers of -1.
If
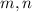 are both even, or if
are both even, or if
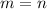 , then
, then
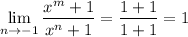
If
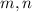 are both odd and
are both odd and
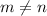 , then we can factorize
, then we can factorize
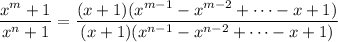
Note that there are
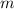 terms in the numerator and
terms in the numerator and
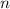 terms in the denominator.
terms in the denominator.
In the limit, the factors of
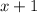 cancel and
cancel and
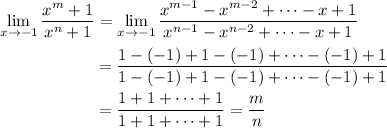
If
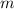 is even and
is even and
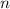 is odd, then we can only factorize the denominator and the discontinuity at
is odd, then we can only factorize the denominator and the discontinuity at
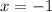 is nonremovable, so
is nonremovable, so
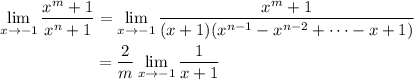
which does not exist.
If
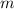 is odd and
is odd and
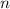 is even, then we can factorize the numerator so that
is even, then we can factorize the numerator so that