Question

An object weighs 63.8 N in air. When it is suspended from a force scale and completely immersed in water the scale reads 16.8 N.

1. Determine the density of the object.
2. When the object is immersed in oil, the force scale reads 35.6 N. Calculate the density of the oil.

Answer 1

The density of this object is approximately
`1.36\; {\rm kg \cdot L^(-1)}`.

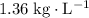The density of the oil in this question is approximately
`0.600\; {\rm kg \cdot L^(-1)}`.

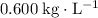(Assumption: the gravitational field strength is
`g =9.806\; {\rm N \cdot kg^(-1)}`)

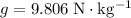Step-by-step explanation:

When the gravitational field strength is
`g`, the weight
`(\text{weight})` of an object of mass
`m` would be
`m\, g`.

Conversely, if the weight of an object is
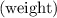`(\text{weight})` in a gravitational field of strength
`g`, the mass
`m` of that object would be
`m = (\text{weight}) / g`.

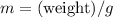Assuming that
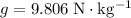`g =9.806\; {\rm N \cdot kg^(-1)}`. The mass of this
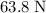`63.8\; {\rm N}`-object would be:

`\begin{aligned} \text{mass} &= \frac{\text{weight}}{g} \\ &= \frac{63.8\; {\rm N}}{9.806\; {\rm N \cdot kg^(-1)}} \\ &\approx 6.506\; {\rm kg}\end{aligned}`.

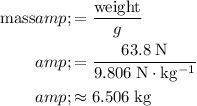When an object is immersed in a liquid, the buoyancy force on that object would be equal to the weight of the liquid that was displaced. For instance, since the object in this question was fully immersed in water, the volume of water displaced would be equal to the volume of this object.

When this object was suspended in water, the buoyancy force on this object was
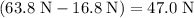`(63.8\; {\rm N} - 16.8\; {\rm N}) = 47.0\; {\rm N}`. Hence, the weight of water that this object displaced would be
`47.0 \; {\rm N}`.

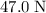The mass of water displaced would be:

`\begin{aligned}\text{mass} &= \frac{\text{weight}}{g} \\ &= \frac{47.0\: {\rm N}}{9.806\; {\rm N \cdot kg^(-1)}} \\ &\approx 4.793\; {\rm kg}\end{aligned}`.

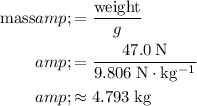The volume of that much water (which this object had displaced) would be:

`\begin{aligned}\text{volume} &= \frac{\text{mass}}{\text{density}} \\ &\approx \frac{4.793\; {\rm kg}}{1.00\; {\rm kg \cdot L^(-1)}} \\ &\approx 4.793\; {\rm L}\end{aligned}`.

Since this object was fully immersed in water, the volume of this object would be equal to the volume of water displaced. Hence, the volume of this object is approximately
`4.793\; {\rm L}`.

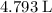The mass of this object is
`6.50\; {\rm kg}`. Hence, the density of this object would be:

`\begin{aligned} \text{density} &= \frac{\text{mass}}{\text{volume}} \\ &\approx \frac{6.506\; {\rm kg}}{4.793\; {\rm L}} \\ &\approx 1.36\; {\rm kg \cdot L^(-1)} \end{aligned}`.

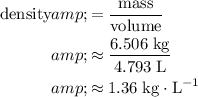(Rounded to
`\text{$3$ sig. fig.}`)

Similarly, since this object was fully immersed in oil, the volume of oil displaced would be equal to the volume of this object: approximately
`4.793\; {\rm L}`.

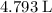The weight of oil displaced would be equal to the magnitude of the buoyancy force:
`63.8\; {\rm N} - 35.6\; {\rm N} = 28.2\; {\rm N}`.

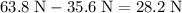The mass of that much oil would be:

`\begin{aligned}\text{mass} &= \frac{\text{weight}}{g} \\ &= \frac{28.2\: {\rm N}}{9.806\; {\rm N \cdot kg^(-1)}} \\ &\approx 2.876\; {\rm kg}\end{aligned}`.

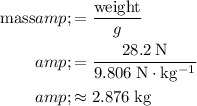Hence, the density of the oil in this question would be:

`\begin{aligned} \text{density} &= \frac{\text{mass}}{\text{volume}} \\ &\approx \frac{2.876\; {\rm kg}}{4.793\; {\rm L}} \\ &\approx 0.600\; {\rm kg \cdot L^(-1)} \end{aligned}`.

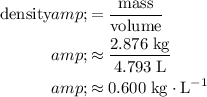(Rounded to
`\text{$3$ sig. fig.}`)