Question

Simplify.
Rewrite the expression in the form y^n.
(y^2)^3 =

Answer 1

`y^6`

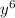
Explanation:

So there is an exponent identity that states:
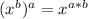`(x^b)^a = x^(a*b)` which means this question becomes:
`(y^2)^3 = y^(2*3) = y^6`.

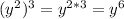Just so you completely understand why this works, it might help to express y^2, as what it truly represents:
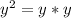`y^2=y*y`. So using this definition we can substitute it into the equation so it becomes:
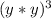`(y*y)^3`. Now let's use the definition of exponents like we just did with the y, to redefine this in terms of multiplication:
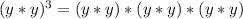`(y*y)^3 = (y * y) * (y * y) * (y * y)`. We can just multiply all these out, and we get:
`y * y * y * y * y * y =y^6`.

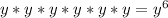To make it a bit more general when we have the exponent:
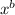`x^b` it can be expressed as:
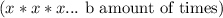`(x*x*x...\text{ b amount of times})` now when we raise it to the power of a. we get:
`(x * x * x...\text{ b amount of times})^a` which can further be rewritten using the definition of an exponent to become the equation:
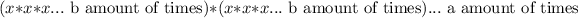`(x*x*x\text... \text{ b amount of times}) * (x * x * x...\text{ b amount of times})...\text{ a amount of times}` which just simplifies to:
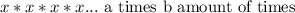`x*x*x*x...\text{ a times b amount of times}`. Hopefully this makes the identity a bit more understandable