Question

Paul flips a fair coin five times. In how many ways can he flip at least three tails?

Answer 1

16

Explanation:

Answer 2

16

Explanation:

We can use the binomial distribution formula to find the probability of flipping three coins tails, four coins tails, and five coins tails. This is because the probability of P(x=3) is going to give the same result if we had defined the entire set, counted how many had 3, and then divided that by the entire set. So we can use this to find how much % of the data set is going to have at least 3.

So the binomial distribution formula is defined as:
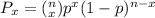`P_x=(^n_x)p^x(1-p)^(n-x)`, where n=number of trials, x=how many successes (in this case it will be 3, 4, and 5) and p=probability of success.

The binomial coefficient is defined as:
`(^n_x)=(n!)/(k!(n-x)!)`.

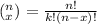So let's define the variables.

x = 3, 4, 5 since we want to find the probability of getting at least 3. This means we want the probability of getting 3, 4, or 5 tails, and then we simply add up these probabilities.

n = 5, since Paul is flipping the coin 5 times

p = 0.5 since the probability of flipping tails is 0.50

So let's plug the information in!

`P_(x\ge3) = P_3 + P_4 + P_5`

`P_3=(5!)/(3!2!)*0.5^30.5^2 = 0.3125`

`P_4=(5!)/(4!1!)*0.5^4*0.5^1=0.15625`

`P_5 = (5!)/(5!0!)0.5^50.5^0 = 0.03125`

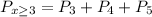
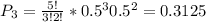
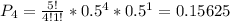
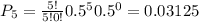
Now let's add up all these probabilities to get:

`0.3125 + 0.15625 + 0.03125 = 0.5`

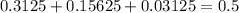
This means 50% of the time Paul will flip three or more tails.

To translate this to the number of ways, we need to find how many combinations there are which can generally be defined as:
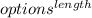`options^(length)` and in this case options = tails and heads so 2, and the length is 5. So we get:
`2^5 = 32`

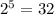
Now multiply the 32 by the 0.5 and you get 16, which is the amount of ways he can flip at least three tails