Question

A 0.41 kg particle moves in an xy plane according to x(t) = - 11 + 1 t - 5 t3 and y(t) = 19 + 3 t - 9 t2, with x and y in meters and t in seconds. At t = 1.4 s, what are (a) the magnitude and (b) the angle (within (-180°, 180°] interval relative to the positive direction of the x axis) of the net force on the particle, and (c) what is the angle of the particle's direction of travel?

Answer 1

It looks like you're given

`x(t) = -11\,\mathrm m + \left(1(\rm m)/(\rm s)\right) t - \left(5(\rm m)/(\mathrm s^3)\right) t^3`

`y(t) = 19\,\mathrm m + \left(3(\rm m)/(\rm s)\right) t - \left(9(\rm m)/(\mathrm s^2)\right) t^2`

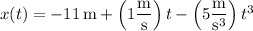
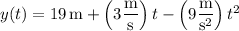
The particle's position vector at time
`t` is given by

`\vec r(t) = x(t)\,\vec\imath + y(t)\,\vec\jmath`

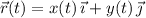
Differentiate
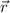`\vec r` twice to recover the velocity and acceleration vectors.

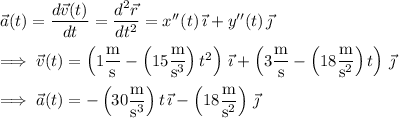
`\vec a(t) = (d\vec v(t))/(dt) = (d^2\vec r)/(dt^2) = x''(t)\,\vec\imath + y''(t)\,\vec\jmath \\\\ \implies \vec v(t) = \left(1(\rm m)/(\rm s) - \left(15(\rm m)/(\mathrm s^3)\right) t^2\right)\,\vec\imath + \left(3(\rm m)/(\rm s) - \left(18(\rm m)/(\mathrm s^2)\right) t\right) \,\vec\jmath \\\\ \implies \vec a(t) = -\left(30(\rm m)/(\mathrm s^3)\right)t \, \vec\imath - \left(18(\rm m)/(\mathrm s^2)\right) \,\vec\jmath`

At
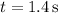`t=1.4\,\rm s`, the particle has acceleration

`\vec a(1.4\,\mathrm s) = \left(-42\,\vec\imath - 18\,\vec\jmath) (\rm m)/(\mathrm s^2)`

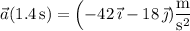
with magnitude

`\|\vec a(1.4\,\mathrm s)\| = \sqrt{\left(-42(\rm m)/(\mathrm s^2)\right)^2 + \left(-18(\rm m)/(\mathrm s^2)\right)^2} \approx 45.695(\rm m)/(\mathrm s^2)`

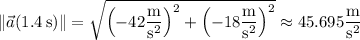
and making an angle
`\theta` relative to the positive
`x`-axis such that

`\tan(\theta) = (-18)/(-42) = \frac37`

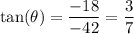
Since both components of the acceleration vector have negative sign, the acceleration points into the third quadrant, so that we add a multiple of 180° after taking the inverse tangent of both sides, namely

`\theta = \tan^(-1)\left(\frac37\right) - 180^\circ \approx -156.801^\circ`

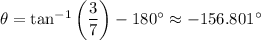
Now, (a) the magnitude of the net force acting on the particle is, by Newton's second law,

`F = (0.41\,\mathrm{kg})\|\vec a(1.4\,\mathrm s)\| \approx \boxed{18.735\,\mathrm N}`

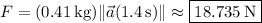
and (b) makes the same angle as the acceleration vector,
`\theta \approx \boxed{-156.801^\circ}`.

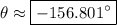At this moment, its velocity vector is

`\vec v(1.4\,\mathrm s) = \left(-28.4\vec\imath - 22.2\,\vec\jmath\right) (\rm m)/(\rm s)`

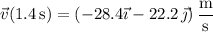
which (c) makes an angle
`\theta` such that

`\tan(\theta) = (-22.2)/(-28.4) = (111)/(142)`

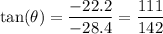
This vector also points in the third quadrant, so

`\theta = \tan^(-1)\left((111)/(142)\right) -180^\circ \approx \boxed{-142.986^\circ}`