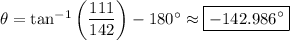It looks like you're given
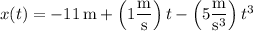
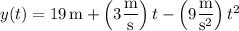
The particle's position vector at time
 is given by
is given by
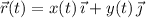
Differentiate
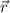 twice to recover the velocity and acceleration vectors.
twice to recover the velocity and acceleration vectors.
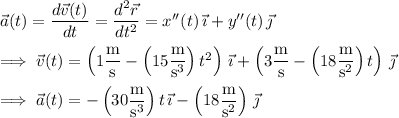
At
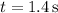 , the particle has acceleration
, the particle has acceleration
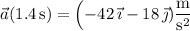
with magnitude
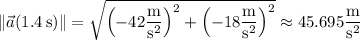
and making an angle
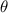 relative to the positive
relative to the positive
 -axis such that
-axis such that
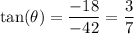
Since both components of the acceleration vector have negative sign, the acceleration points into the third quadrant, so that we add a multiple of 180° after taking the inverse tangent of both sides, namely
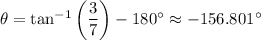
Now, (a) the magnitude of the net force acting on the particle is, by Newton's second law,
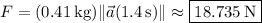
and (b) makes the same angle as the acceleration vector,
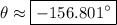 .
.
At this moment, its velocity vector is
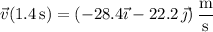
which (c) makes an angle
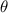 such that
such that
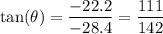
This vector also points in the third quadrant, so