Question

Which expressions represent the sum of exactly two terms?

Choose 2 answers:
A. xy
B. m^4+6m
C. 3+7s+t
D. a+c

Answer 1

Answer: D and B

Explanation:

Formula for two terms = a + b

Therefore,

D and B have two terms aka one plus sign

D. a + c

B. m^4 + 6m

Answer 2

Hi! ❄

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

The sum of two terms is what we get after adding these two terms.

If you add two positive terms, you put a + sign in between these terms.

`\sf{Example\!\!:a+b}`

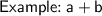
If you add two negative terms, you put a - sign in between these terms.

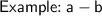`\sf{Example\!\!:a-b}` (this is the same as
`\sf{a+-b}`)

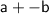Let's look at the provided choices to see which one works.

Choice A.

• Provided Expression =
  `\sf{xy}`
• Does Choice A. work ??

It doesn't, because
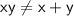`\sf{xy\\eq x+y}`. In this expression a number x was multiplied by a number y. So this one doesn't check.

One down, three to go.

Choice B.

• Provided Expression =
  `\sf{m^4+6m}`
• Does Choice B. work ??

It does, because
`\sf{m^4+6m\stackrel\checkmark{=}m^4+6m}`. A number m was multiplied by itself 4 times, and then the product of that samee number m and 6 was added to it.

So this one checks.

Choice C.

• Provided Expression =
  `\sf{3+7s+t}`
• Does Choice C. work ??

It doesn't. It is indeed a sum, but we need 2 terms, not 3

So this one doesn't work.

Choice D.

• Provided Expression =
  `\sf{a+c}`
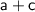
• Does Choice D. work ??

It does, because
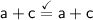`\sf{a+c\stackrel\checkmark{=}a+c}`. So Choice D. also works.

Hope that made sense !!

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

`\star\tiny\pmb{calligraphy}\star`