Hi! ❄
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
The sum of two terms is what we get after adding these two terms.
If you add two positive terms, you put a + sign in between these terms.
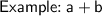
If you add two negative terms, you put a - sign in between these terms.
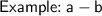 (this is the same as
(this is the same as
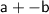 )
)
Let's look at the provided choices to see which one works.
Choice A.
- Provided Expression =
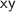
- Does Choice A. work ??
It doesn't, because
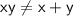 . In this expression a number x was multiplied by a number y. So this one doesn't check.
. In this expression a number x was multiplied by a number y. So this one doesn't check.
One down, three to go.
Choice B.
- Provided Expression =

- Does Choice B. work ??
It does, because
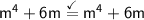 . A number m was multiplied by itself 4 times, and then the product of that samee number m and 6 was added to it.
. A number m was multiplied by itself 4 times, and then the product of that samee number m and 6 was added to it.
So this one checks.
Choice C.
- Provided Expression =
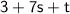
- Does Choice C. work ??
It doesn't. It is indeed a sum, but we need 2 terms, not 3
So this one doesn't work.
Choice D.
- Provided Expression =
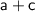
- Does Choice D. work ??
It does, because
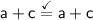 . So Choice D. also works.
. So Choice D. also works.
Hope that made sense !!
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -