Answer: See the attached image below for the filled in table.
=========================================================
Step-by-step explanation:
The domain is the set of all allowed x inputs of a function.
The term "radicand" refers to the stuff under the square root.
We cannot have a negative number under the square root. Therefore, the radicand must be 0 or larger.
The first function must have
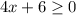 which becomes
which becomes
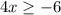 and leads to
and leads to
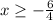 aka
aka

So x = -3/2 is the smallest input allowed. Which is where the interval notation of
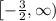 comes from. It's the interval spanning from -3/2 (inclusive) to infinity. This represents the set of all possible x inputs of the first function.
comes from. It's the interval spanning from -3/2 (inclusive) to infinity. This represents the set of all possible x inputs of the first function.
--------
Follow this same idea for problem 2. The steps would be something like this:

The inequality sign flips because we divided both sides by a negative number. That then leads to the interval notation of
![(-\infty, -(3)/(10)\big]](https://img.qammunity.org/2023/formulas/mathematics/high-school/k8lauy13wbvvwp4toybnyb4txar69qekk8.png)
The interval spans from negative infinity (exclusive) to -3/10 (inclusive).
--------
Problem 3 would have these steps
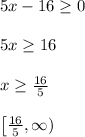
No sign flip happens since we divided both sides by a positive number.
--------
Lastly, here are the steps for problem 4
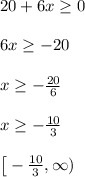
Don't forget to use the square bracket to include the endpoints mentioned. We always use curved parenthesis for either infinity because we can't ever reach infinity. In a sense, we "approach" infinity.
Once again, all of this is summarized in the filled out table shown below (attached image). Feel free to ask any questions if they come to mind.