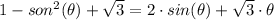The given function for the difference in length is presented as follows;
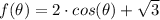
When the pogo stick will be equal to its non compressed length, the difference is zero, therefore;
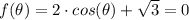
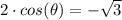
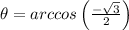
Which gives;


Part B; If the angle was doubled, we have;

Therefore;
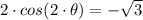
Which gives;
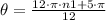
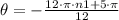
Between 0 and 2•π, we have;
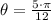
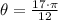
Part C;
The toddler's pogo stick is presented as follows;
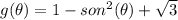
Integrating the original function between 0 and theta gives;
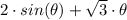
The original length =
Therefore, when the lengths are equal, we have;