Answer: H
Explanation:
Finding the Diameter
If we draw a line through a diagonal of the square, two triangles are formed. The angle opposite the diagonal is 90°, as all angles are 90° in a square. One of the properties of a circle state that the angle in a semicircle is always 90°, which means that the diagonal formed a semi-circle.
A semi-circle only forms when a diameter is drawn in a circle, making the diagonal a diameter. This will be useful information, as we can calculate the side length of a square using the length of its diagonal.
A diameter is just twice the length of a radius, so the diagonal of the square would be 6 cm.
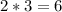
Finding the Length of One Side
The diagonal also splits the square into two 45-45-90 triangles. These triangles have a special property that their hypotenuse is √2 times each leg, and all legs are the same length.
Therefore, we can calculate the length of a leg by dividing the hypotenuse by √2.
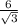
The length of one side of the square is
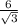
Finding the Area
As we already know the length of one side, we can just square it to get the area.
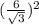
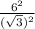 [Properties of Exponents]
[Properties of Exponents]

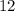
Hence, the area of the square is 12 cm².