Answer:
w = ±
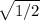 or w= ±
or w= ±

Explanation:
if we say some variable y = w^2, we can rewrite the equation to:
2y^2 - 5y + 2 = 0
this can be factored into (2y-1)(y-2) = 0
putting w^2 back in the place of y, that's (2w^2 - 1)(w^2 - 2) = 0
The equation is a fourth degree polynomial, so there are four roots, or four values of w that will cause the equation to equal 0.
If 0 is multiplied by anything, the result is 0, so we set 2w^2 - 1 = 0 and solve for w, which is ±√1/2, then set w^2 - 2 = 0 to get w = ±√2 as our roots
the four solutions are ±√1/2 and ±√2
(because the positive counts as one solution and the negative another solution)