Question

Find the area of the segment (unshaded area) of Circle G with radius 4in. Round to the nearest tenth.

Answer 1

Angle is 90°

The sector is 1/4 th of circle

Area of sector

• πr²/4
• π(4)²/4
• 4πin²

Triangle is right angled

Area

• 1/2(4)²
• 16/2
• 8in²

Area of unshaded region

• 4π-8
• 4(π-2)
• 4(3.14-2)
• 4(1.14)
• 4.56in²

Answer 2

4.6 in² (nearest tenth)

Explanation:

To find the area of the unshaded region, subtract the area of ΔAGB from the area of sector AGB.

The measure of an arc is equal to its corresponding central angle measure. Therefore, the central angle of sector AGB is 90°.

As the two sides of ΔAGB adjacent the central angle are the radii of the circle they are therefore equal in length ⇒ ∠GAB = ∠GBA.

Therefore, ΔAGB is an isosceles triangle.

Area of triangle (using the Sine Rule):

`\sf A=(1)/(2)ab \sin C`

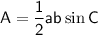
(where a and b are the side lengths and C is the included angle)

Given:

• a = b = radius = 4 in
• C = 90°

`\implies \sf Area\:of\:triangle=(1)/(2)(4)(4)\sin 90^(\circ)=8\:in^2`

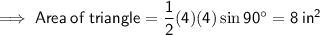
Area of a sector of a circle

`\textsf{A}=\left((\theta)/(360^(\circ))\right) \pi r^2`

`\textsf{(where r is the radius and the angle }\theta \textsf{ is measured in degrees)}`

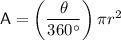
Substituting the given angle and radius:

`\implies \textsf{A}=\left((90^(\circ))/(360^(\circ))\right) \pi (4)^2=4\pi\:\: \sf in^2`

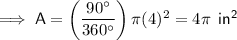
Area of the unshaded region:

`\begin{aligned}\textsf{Area of unshaded region} & =\textsf{Area of sector} - \textsf{Area of triangle}\\& = 4 \pi - 8\\& = 4.566370614...\\ & = 4.6\:\sf in^2\:\:(nearest\:tenth)\end{aligned}`