Question

Given Circle G with radius r, what is the formula for the area of the segment (unshaded region)

Answer 1

Option D

Explanation:

The triangle ABJ is equitorial

So area

• √3/4r²

Then mBJ is a arc which is 1/6th of circle

Area.

• π/6r²

So area of unshaded region

• πr²/6-√3/4r²
• r²(π/6-√3/4)

Answer 2

`\textsf{d.} \quad r^2\left((\pi)/(6)- (√(3))/(4)\right)`

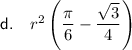
Explanation:

To find the area of the unshaded region, subtract the area of ΔJGB from the area of sector JGB.

The measure of an arc is equal to its corresponding central angle measure. Therefore, the central angle of sector JGB is 60°.

As the two sides of ΔJGB adjacent the central angle are the radii of the circle (and therefore equal in length), ∠GJB = ∠GBJ.

Interior angles of a triangle sum to 180°. Therefore, all interior angles of ΔJGB are 60° which makes it an equilateral triangle.

Area of an equilateral triangle:

`\sf A=(√(3))/(4)a^2 \quad \textsf{(where a is the side length)}`

As the side length of the given equilateral triangle is the radius (r):

`\implies \sf Area\:of\:triangle=(√(3))/(4)r^2`

To find the area of the sector, first convert degrees to radians by multiplying the degrees by π/180 :

`\implies 60^(\circ)=60 * ( \pi)/(180)=(\pi)/(3)\:\:\sf radians`

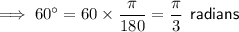
Area of a sector of a circle

`\textsf{A}=\frac12 r^2 \theta \quad \textsf{(where r is the radius and the angle }\theta \textsf{ is in radians)}`

Substituting the angle in radians, the area of the sector is:

`\implies \sf A=(1)/(2)r^2\left((\pi)/(3)\right)`

`\implies \sf A=\frac{\pi}6}r^2`

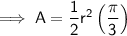
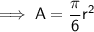
Area of the unshaded region:

`\begin{aligned}\textsf{Area of unshaded region} & =\textsf{Area of sector} - \textsf{Area of triangle}\\\\& = (\pi)/(6)r^2 - (√(3))/(4)r^2\\\\& = r^2\left((\pi)/(6)- (√(3))/(4)\right)\end{aligned}`

Therefore, the solution is option D.