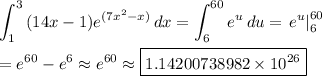Question

Could you help me solve?

Answer 1

1.14200738982×10^26

Explanation:

Substitution can make this integral much easier to evaluate.

Substitution

Let u = 7x² -x. Then du = (14x -1)dx. The limits on x become different limits for u:

for x = 1: u = 7(1²) -1 = 6

for x = 3: u = 7(3²) -3 = 60

Integral

`\displaystyle\int_1^3{(14x-1)e^((7x^2-x))}\,dx=\int_6^(60){e^u}\,du=\left.e^u\right|^(60)_6\\\\=e^(60)-e^6\approx e^(60)\approx\boxed{1.14200738982*10^(26)}`