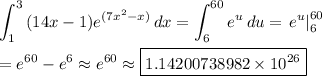Answer:
1.14200738982×10^26
Explanation:
Substitution can make this integral much easier to evaluate.
Substitution
Let u = 7x² -x. Then du = (14x -1)dx. The limits on x become different limits for u:
for x = 1: u = 7(1²) -1 = 6
for x = 3: u = 7(3²) -3 = 60
Integral