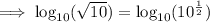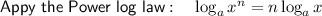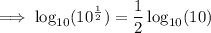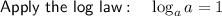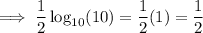Question

MATH HELP!!! 100PTS!!!

Suppose that u=log10(3) and v=log10(5). Find possible formulas for the following expressions in terms of u and/or v. Your answers should NOT involve any log 's.

a) log10(0.6)=
u-v


b) log10(0.25)=



c) log10(27000)=
3+3u


d) log10(sqrt10)=

Answer 1

a) u - v

b) 2v - 2

c) 3u + 3

d) ¹/₂

Explanation:

Given:

`u=\log_(10)3`

`v=\log_(10)5`

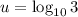
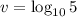
Part (a)

Rewrite 0.6 as a fraction:

`\implies \log_(10)(0.6)=\log_(10)\left((3)/(5)\right)`

`\textsf{Apply the quotient log law}: \quad \log_a(x)/(y)=\log_ax - \log_ay:`

`\implies \log_(10)\left((3)/(5)\right)=\log_(10)3-\log_(10)5`

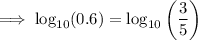
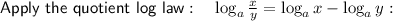
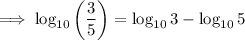
Substitute the values of u and v:

`\implies \log_(10)3-\log_(10)5=u-v`

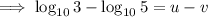
Part (b)

Rewrite 0.25 as 25/100:

`\implies \log_(10)(0.25)=\log_(10)\left((25)/(100)\right)`

`\textsf{Apply the quotient log law}: \quad \log_a(x)/(y)=\log_ax - \log_ay`

`\implies \log_(10)\left((25)/(100)\right)=\log_(10)(25)-\log_(10)(100)`

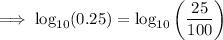
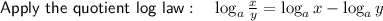
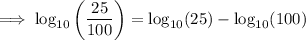
Rewrite 25 as 5² and 100 as 10²:

`\implies \log_(10)(25)-\log_(10)(100)=\log_(10)(5^2)-\log_(10)(10^2)`

`\textsf{Appy the Power log law}: \quad \log_ax^n=n\log_ax`

`\implies \log_(10)(5^2)-\log_(10)(10^2)=2\log_(10)5-2\log_(10)10`

`\textsf{Apply the log law}: \quad \log_aa=1`

`\implies 2\log_(10)5-2\log_(10)10=2\log_(10)5-2(1)`

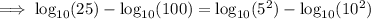
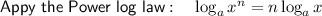
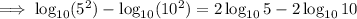
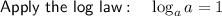
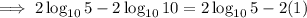
Substitute the value of v:

`\implies 2\log_(10)5-2(1)=2v-2`

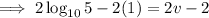
Part (c)

Rewrite 27000 as 30³:

`\implies \log_(10)(27000)=\log_(10)(30^3)`

`\textsf{Appy the Power log law}: \quad \log_ax^n=n\log_ax`

`\implies \log_(10)(30^3)=3\log_(10)(30)`

`\textsf{Apply the log product law}: \quad \log_axy=\log_ax + \log_ay`

`\implies 3\log_(10)(30)=3\log_(10)(3)+3\log_(10)(10)`

`\textsf{Apply the log law}: \quad \log_aa=1`

`\implies 3\log_(10)(3)+3\log_(10)(10)=3\log_(10)(3)+3(1)`

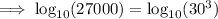
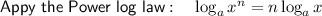
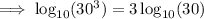
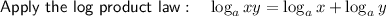
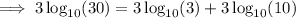
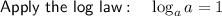
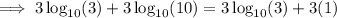
Substitute the value of u:

`\implies 3\log_(10)(3)+3(1)=3u+3`

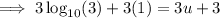
Part (d)

Rewrite √10 as
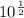`10^{(1)/(2)}` :

`\implies \log_(10)(√(10))=\log_(10)(10^{(1)/(2)})`

`\textsf{Appy the Power log law}: \quad \log_ax^n=n\log_ax`

`\implies \log_(10)(10^{(1)/(2)})=(1)/(2)\log_(10)(10)`

`\textsf{Apply the log law}: \quad \log_aa=1`

`\implies (1)/(2)\log_(10)(10)=(1)/(2)(1)=(1)/(2)`