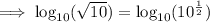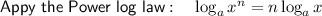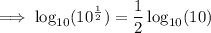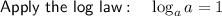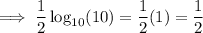Answer:
a) u - v
b) 2v - 2
c) 3u + 3
d) ¹/₂
Explanation:
Given:
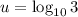
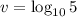
Part (a)
Rewrite 0.6 as a fraction:
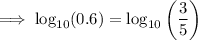
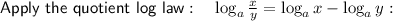
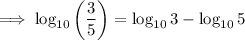
Substitute the values of u and v:
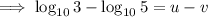
Part (b)
Rewrite 0.25 as 25/100:
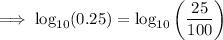
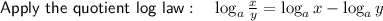
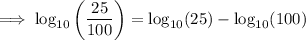
Rewrite 25 as 5² and 100 as 10²:
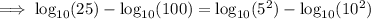
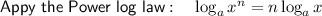
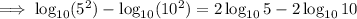
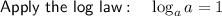
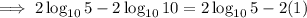
Substitute the value of v:
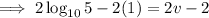
Part (c)
Rewrite 27000 as 30³:
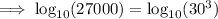
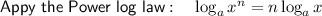
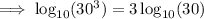
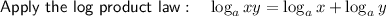
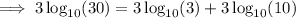
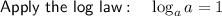
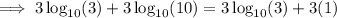
Substitute the value of u:
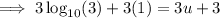
Part (d)
Rewrite √10 as
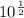 :
: