Answer:
x =
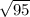
Explanation:
In this problem, we need to use the Pythagorean theorem.
Pythagorean theorem is a theorem where you can find a side length in a right triangle.
The hypotenuse (The longest side) squared equals the other two side lengths added together after being squared.
In numbers, this will be: (12)^2 = (7)^2 + (x)^2.
144 = 49 + x^2.
95 = x^2
x =
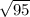
We cannot simplify
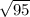 , so that is the final answer.
, so that is the final answer.