Question

A test requires that you answer first Part A and then either Part B or Part C. Part A consists of 6 true-false questions, Part B consists of 6 multiple-choice questions with one correct answer out of five, and Part C consists of 3 multiple-choice questions with one correct answer out of six. How many different completed answer sheets are possible?

Answer 1

1,013,824 different completed answer sheets are possible

Explanation:

So let's start with part A. There is 6 questions which have 2 options, because it's a true-false question. With the first question, you can choose 2 options, true or false, from there you can choose true or false. I've attached a diagram which further illustrates this. So as you can see as you answer each question, the amount of combinations get's multiplied by 2, or in other words, the amount of combinations can be expressed as:
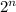`2^n` where n=amount of questions. Since there are 6, there are
`2^6` combinations which is 64 total combinations by the time you answer all 6 questions.

So now from here you can choose either part B or C, and I'm assuming you can't do both, you chose one. So we can treat them as completely separate scenarios, and then after that add the amount of combinations from doing part A/B and part A/C.

So let's start with the scenario that you do part B after part A. part B consists of 6 multiply choice questions and it has 5 options per question. If you remember, the first question, you had 2 initial options, and for each of those 2 initial options, you had 2 more (true/false), then you had 4, then for each of those 4 you had 2, then you had 8. So this relationship can generally be treated as:
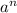`a^n` where a = amount of options, and n = amount of questions. This is because for each question, you're going to have a options, so the first question is going to be "a" amount of combinations, then the second question, for each combination which is currently a, you're going to have "a" combinations, so now you have a*a combinations and so on... So here you're going to have:
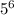`5^6` choices. which is 15,625. But remember, this is after doing part A. So this means you can extend these amount of combinations to the 64 amount of combinations. I attached another graph to help you understand this. This means you will have 15,625 * 64 combinations which is 1,000,000 combinations if you chose part A then part B

Now let's look at the scenario you chose part A then part C. This isn't an extension onto part B, so we can see them as two separate scenarios. So like two completely different graphs. So for part C, we can use the general equation we used in the previous question:
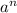`a^n`. In this case there are 3 questions, and 6 options, so the amount of combinations is:
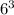`6^3` which is 216, now for reasons explained in the previous paragraph, you need to multiply this by the 64 combinations from part A. This gives you 216 * 64 = 13,824.

So now we calculated part A/B combinations = 1,000,000

and part A/C combinations = 13,824

So adding these together you get: 1,013,824 combinations