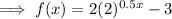Answer:

Explanation:
Parent function:

Properties of the given parent function:
- y-intercept at (0, 1)
- horizontal asymptote at y = 0
- As x → -∞, y → 0
- As x → ∞, y → ∞
Given form of function f(x):
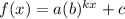
If the parent function is
 then b = 2:
then b = 2:
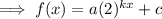
From inspection of the graphed function f(x):
- y-intercept at (0, -1)
- horizontal asymptote at y = -3
Therefore, the y-intercept has shifted 2 units down, yet the asymptote has shifted 3 units down. This implies that there has been a vertical shift of 3 units down and a vertical stretch.
The vertical shift is denoted by the variable "c" so c = -3:
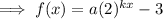
The vertical stretch is denoted by the variable "a". To find value of a, substitute the point of the y-intercept into the equation:
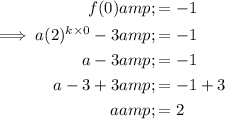
Therefore, as a = 2:
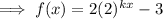
From inspection of the given graph, the curve passes through point (4, 5). Substitute this point into the equation to find the value of k:
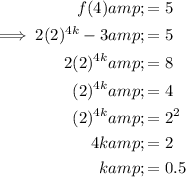
Therefore, the equation of the function f(x) is: