Answer:
The 14th term of arithmetic sequence is -107.
Explanation:
Here's the required formula to find the arithmetic sequence :
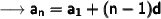
 aₙ = nᵗʰ term in the sequence
aₙ = nᵗʰ term in the sequence
 a₁ = first term in sequence
a₁ = first term in sequence
 n = number of terms
n = number of terms
 d = common difference
d = common difference
Substituting all the given values in the formula to find the 14th term of arithmetic sequence :
 aₙ = a₁₄
aₙ = a₁₄
 a₁ = 10
a₁ = 10
 n = 14
n = 14
 d = -9
d = -9
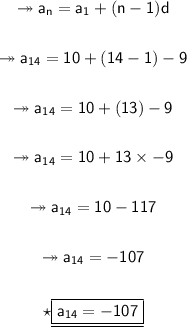
Hence, the 14th term of arithmetic sequence is -107.
