Given:
The boundary line of an inequality is:
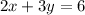
The solution set contains (0,0).
To find:
The inequality.
Solution:
The boundary line of an inequality is
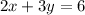
Since (0,0) is in the solution set, therefore (0,0) satisfies the required inequality.
Taking LHS, we get
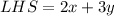
Substitute x=0 and y=0.

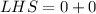

The right hand side of the given equation is 6.
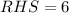
We know that,
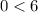
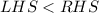
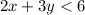
The boundary line is not a dotted line, it means the points on the boundary line are also included in the solution set. So, the inequality sign must be
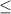 .
.
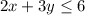
Therefore, the required inequality is
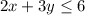 .
.