1 Answer

Jscoot · Answer 1 · 2022-12-29T13:13:26+0000

Given:

Mean = 45

Standard deviation = 9

Confidence level = 95%.

To find:

The confidence interval.

Solution:

The formula for confidence interval is:

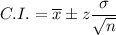
$C.I.=\overline{x}\pm z(\sigma)/(√(n))$

Where,
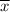$\overline{x}$ is mean, z is the z-value at given level of confidence,
$\sigma$ is the standard deviation and n is the number of observations.

The z-value at 95% confidence level is 1.96.

Here number of observations are not given. Assume it is 1.

Putting
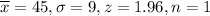$\overline{x}=45,\sigma=9,z=1.96,n=1$ .

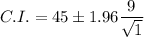
$C.I.=45\pm 1.96(9)/(√(1))$

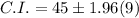
$C.I.=45\pm 1.96(9)$

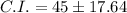
$C.I.=45\pm 17.64$

It can be written as

C.I.=[45-17.64,45+17.64]

C.I.=[27.36,62.64]

Approximate the value to the nearest whole number.

C.I.=[27,63]

The interval for the middle 95% of snowfall is 27 to 63.

Therefore, the correct option is A.

Please log in or register to add a comment.