Answer:
3,4.
Explanation:
Solving a quadratic equation:
Given a second order polynomial expressed by the following equation:
 .
.
This polynomial has roots
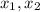 such that
such that
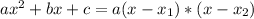 , given by the following formulas:
, given by the following formulas:

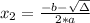
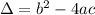
In this question:
The function is:
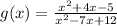
In a fraction, the values not in domain are the values for which the denominator is 0.
Find all values of that are NOT in the domain of g.
It will not be in domain if the denominator is 0. So

That is, a quadratic equation with
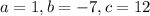

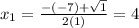
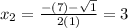
The values are 3 and 4, so the answer is 3,4.