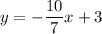Answer:
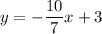
Explanation:
We want to find the equation of the line that includes the points (7, -7) and (0, 3).
First, we will find the slope of the line using the slope formula given by:

So, the slope of our line is:
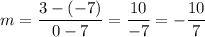
Next, notice that the given point (0, 3) is our y-intercept.
Slope-intercept form is given by:

Where m is the slope and b is the y-intercept.
Therefore, by substitution, we acquire that our equation is: