Answer:
as a decimal:
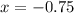
as a fraction:
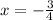
Explanation:
note: i'm going to convert the fractions to decimals because i prefer working with decimals rather than fractions :)
 as a decimal is
as a decimal is
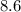
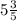 as a decimal is
as a decimal is
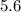
- the equation is now
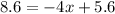
first, subtract 5.6 from both sides of the equation.
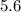 and
and
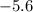 cancel each other out, leaving you with
cancel each other out, leaving you with
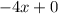 on the right side of the equation. it's not necessary to leave the
on the right side of the equation. it's not necessary to leave the
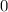 in the equation, so just leave it as
in the equation, so just leave it as
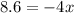
- now subtract
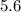 from the left side of the equation.
from the left side of the equation.
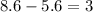 , therefore the equation is now
, therefore the equation is now

then divide both sides of the equation by -4.
- you are left with
 on the right side of the equation and
on the right side of the equation and
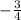 or
or
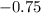 on the left side of the equation, aka
on the left side of the equation, aka
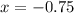 or
or
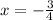
and that's it! the solution as a fraction is
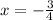 and as a decimal is
and as a decimal is
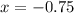 .
.
if you want to check the solution, just plug one of those values in for
 in the original equation. since i converted it all to decimals, i'll check my answer using
in the original equation. since i converted it all to decimals, i'll check my answer using
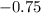 for
for
 in
in
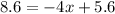 .
.
first, plug in -0.75 for x.
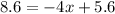 ⇒
⇒
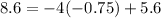
begin simplifying by multiplying -4 and -0.75.
add 3 and 5.6.
since both sides of the equation are equal, that means your
 value is correct and therefore a solution to the equation!! :)
value is correct and therefore a solution to the equation!! :)
i hope this helped! have a lovely rest of your day <3