Answer:
The velocity at section is approximately 42.2 m/s
Step-by-step explanation:
For the water flowing through the pipe, we have;
The pressure at section (1), P₁ = 300 kPa
The pressure at section (2), P₂ = 100 kPa
The diameter at section (1), D₁ = 0.1 m
The height of section (1) above section (2), D₂ = 50 m
The velocity at section (1), v₁ = 20 m/s
Let 'v₂' represent the velocity at section (2)
According to Bernoulli's equation, we have;

Where;
ρ = The density of water = 997 kg/m³
g = The acceleration due to gravity = 9.8 m/s²
z₁ = 50 m
z₂ = The reference = 0 m
By plugging in the values, we have;
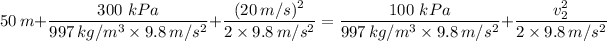 50 m + 30.704358 m + 20.4081633 m = 10.234786 m +
50 m + 30.704358 m + 20.4081633 m = 10.234786 m +
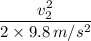
50 m + 30.704358 m + 20.4081633 m - 10.234786 m =
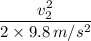
90.8777353 m =
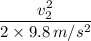
v₂² = 2 × 9.8 m/s² × 90.8777353 m
v₂² = 1,781.20361 m²/s²
v₂ = √(1,781.20361 m²/s²) ≈ 42.204308 m/s
The velocity at section (2), v₂ ≈ 42.2 m/s