Answer:
The age of the pottery bowl is 10523 years.
Explanation:
Amount of substance:
The amount of a substance after t years is given by the following equation:
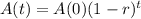
In which A(0) is the initial amount and r is the decay rate.
Half-life of C14.
Researching, the half-life of c-14 is 5730 years.
This means that:
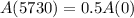
We use this to find r. So
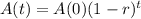
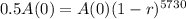
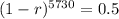
![\sqrt[5730]{(1-r)^(5730)} = \sqrt[5730]{0.5}](https://img.qammunity.org/2022/formulas/mathematics/high-school/jx4kao9fclz6udus3wxpsclakhjzxcr5cf.png)
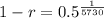
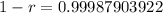
So
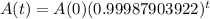
Age of the pottery bowl:
We have that:
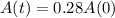
We have to find t. So
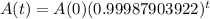
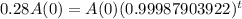
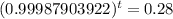
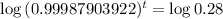

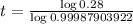
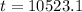
So
The age of the pottery bowl is 10523 years.