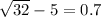Solve by completing the square. Round your answers to the nearest tenth and then locate the greater solution. x^(2)+10x-7=0

Question

Solve by completing the square. Round your answers to the nearest tenth and then locate the greater solution.
`x^(2)`+10x-7=0

Answer 1

Explanation:

Step 1: Write our Givens

`{x}^(2) + 10x - 7 = 0`

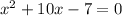
Move the constant term ,(the term with no variable) to the right side.

Here we have a negative 7, so we add 7 to both sides

`{x}^(2) + 10x = 7`

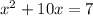
Next, we take the linear coeffeicent and divide it by 2 then square it.

`( (10)/(2) ) {}^(2) = 25`

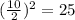
Then we add that to both sides

`{x}^(2) + 10x + 25 = 7 + 25`

`{ {x}^(2) } + 10x + 25 = 32`

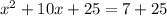
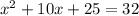
Next, we factor the left,

`(x + 5)(x + 5) = 32`

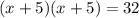
we got 5 because 5 add to 10 and multiply to 25 as well.

so we get

`(x + 5) {}^(2) = 32`

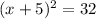
This is called a perfect square trinomial.

Next, we take the square root of both sides

`x + 5 = ± √(32)`

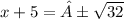
± menas that we have a positive and negative solution.

Subtract 5 form both side so we get

`x = - 5± √(32)`

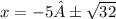
The greater solution is when sqr root of 32 is positive so the answer to that is

`√(32) - 5 = 0.7`