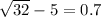Explanation:
Step 1: Write our Givens
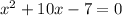
Move the constant term ,(the term with no variable) to the right side.
Here we have a negative 7, so we add 7 to both sides
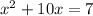
Next, we take the linear coeffeicent and divide it by 2 then square it.
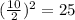
Then we add that to both sides
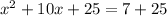

Next, we factor the left,
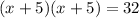
we got 5 because 5 add to 10 and multiply to 25 as well.
so we get
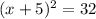
This is called a perfect square trinomial.
Next, we take the square root of both sides
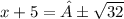
± menas that we have a positive and negative solution.
Subtract 5 form both side so we get
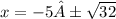
The greater solution is when sqr root of 32 is positive so the answer to that is