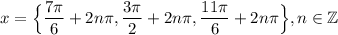Question

I need to solve the equation please help me

Answer 1

`\displaystyle x=\Big\{(7\pi)/(6)+2n\pi, (3\pi)/(2)+2n\pi, (11\pi)/(6)+2n\pi}\Big\}, n\in\mathbb{Z}`

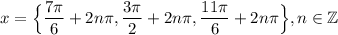
Explanation:

We are given the equation:

`4\sin^2(x)+6\sin(x)+2=0`

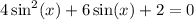
First, we can divide everything by 2:

`2\sin^2(x)+3\sin(x)+1=0`

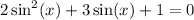
Notice that we have an equation in quadratic form. Namely, if we make a substitution where u = sin(x), we acquire:

`2u^2+3u+1=0`

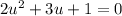
Solve for u. Factor:

`(2u+1)(u+1)=0`

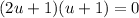
Zero Product Property:

`2u+1=0\text{ or } u+1=0`

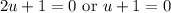
Solving for both cases:

`\displaystyle u=-(1)/(2)\text{ or } u=-1`

And by substitution:

`\displaystyle \sin(x)=-(1)/(2)\text{ or } \sin(x)=-1`

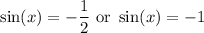
For the first case, recall that sin(x) is -1/2 for every 7π/6 and every 11π/6. Hence, for the first case, our solutions are:

`\displaystyle x=(7\pi)/(6)+2n\pi \text{ and } x=(11\pi)/(6)+2n\pi, n\in\mathbb{Z}`

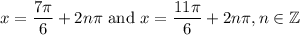
Where n is an integer.

For the second case, sin(x) is -1 for every 3π/2. Thus:

`\displaystyle x=(3\pi)/(2)+2n\pi`

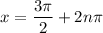
All together, our solutions are:

`\displaystyle x=\Big\{(7\pi)/(6)+2n\pi, (3\pi)/(2)+2n\pi, (11\pi)/(6)+2n\pi}\Big\}, n\in\mathbb{Z}`