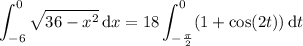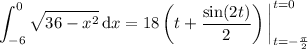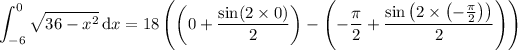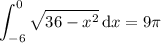I think how you approach this depends on your knowledge of calculus.
If you don't know how to compute definite integrals yet, but you do know that they represent signed areas under curves, then you can plot both curves |x - 4| and √(36 - x ²), then recognize that the areas represented by these integrals are areas of geometric shapes. (See attached images)
First integral: if you plot |x - 4| on the interval [3, 6], you'll see that the integral corresponds to the area of two triangles. One of them has base = height = 1, and the other has base = height = 2. Then
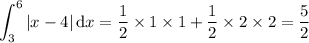
Second integral: if
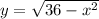 , then
, then
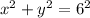 , meaning this curve is the upper half of a circle with radius 6. On the interval [-6, 0], the area amounts to 1/4 of the total area of such a circle, so that
, meaning this curve is the upper half of a circle with radius 6. On the interval [-6, 0], the area amounts to 1/4 of the total area of such a circle, so that
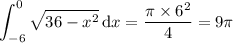
* * *
If you already know a few things about calculus and integration, you can compute these areas directly.
First integral:
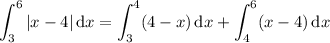
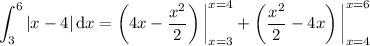
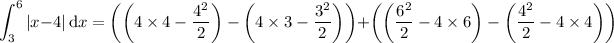
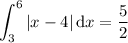
Second integral:
Substitute x = 6 sin(t ) and dx = 6 cos(t ) dt, then
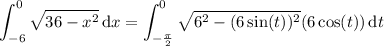
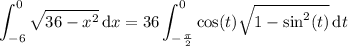
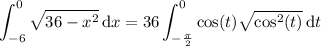
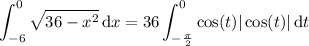
For t ∈ [-π/2, 0], cos(t ) > 0, so |cos(t )| = cos(t ) :
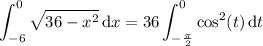
Recall the half-angle identity,
cos²(t ) = (1 + cos(2t )) / 2