Question

I need help with this problem

Answer 1

at x = 1 we have one tangent line and at x = 5 we have just another tangent line.

`f(x)=3x^2-15x\implies \left. \cfrac{df}{dx}=6x-15 \right|_(x=1)\implies \stackrel{\stackrel{m}{\downarrow }}{-9}~\hfill \left. 6x-15\cfrac{}{} \right|_(x=5)\implies \stackrel{\stackrel{m}{\downarrow }}{15}`

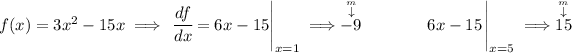
so we have the slopes, but what about the coordinates?

well, for the first one we know x = 1 and we also know f(x), let's use f(1) to get "y", and likewise we'll do the for the second one.

`\stackrel{x=1}{f(1)}=3(1)^2-15(1)\implies f(1)=-12\qquad \qquad (\stackrel{x_1}{1}~~,~~\stackrel{y_1}{-12}) \\\\\\ \begin{array} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{(-12)}=\stackrel{m}{-9}(x-\stackrel{x_1}{1}) \\\\\\ y+12=-9x+9\implies y=-9x-3 \\\\[-0.35em] ~\dotfill`

`\stackrel{x=5}{f(5)}=3(5)^2-15(5)\implies f(5)=0\qquad (\stackrel{x_1}{5}~~,~~\stackrel{y_1}{0}) \\\\\\ \begin{array}c \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{0}=\stackrel{m}{15}(x-\stackrel{x_1}{5})\implies y=15x-75`